本篇目录:
急需勾股定理论文800字
1、数学勾股定理小论文篇一 “兴趣是最好的老师。”在勾股定理的日常教学中,我们要注重学生兴趣的激发。
2、勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。

3、而这次我们要探究的“勾股定理”就隐藏在直角三角形中。 直角三角形中有一个直角,夹着直角的那两条边我们称之为直角边,而另外的一条边我们称之为斜边。
4、五年级数学小论文:勾股定理 证明一个三角形是直角三角形 用于直角三角形中的相关计算 有利于你记住余弦定理,它是余弦定理的一种特殊情况。
关于勾股定理证明的小论文400字左右
1、数学勾股定理小论文篇一 “兴趣是最好的老师。”在勾股定理的日常教学中,我们要注重学生兴趣的激发。
2、我国历代数学家关于勾股定理的论证方法有多种,为勾股定理作的图注也不少,其中较早的是赵爽(即赵君卿)在他附于《周髀算经》之中的论文《勾股圆方图注》中的证明。
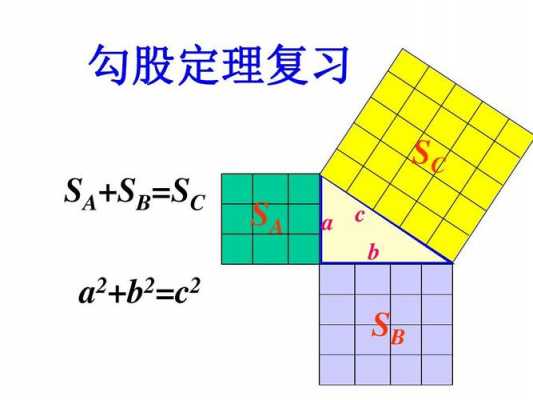
3、证明过程如下。 这样我们就可以证明出如果三角形的三边长a、b、c满足 a方加 b方等于c方时,那么这个三角形就是一个直角三角形,我们称其为勾股定理之逆定理。
4、年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑,其中收集了367种不同的证明方法。实际上还不止于此,有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
5、赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。在这幅“勾股圆方图”中,以弦为边长得到正方形ABDE是由4个相等的直角三角形再加上中间的那个小正方形组成的。
6、五年级数学小论文:勾股定理 证明一个三角形是直角三角形 用于直角三角形中的相关计算 有利于你记住余弦定理,它是余弦定理的一种特殊情况。

写一篇关于学习勾股定理后的一点感受。
1、这说明,勾股定理实际上早已进入了人类知识的宝库。
2、在直角三角形中 一条直角边的平方加上另一条直角边的平方 等于这个三角形斜边也就是最长边的平方 勾股定理对以后学习三角函数很有帮助。
3、学习了勾股定理以后,我发现了一些有规律的事,比如说:5,12,13,4,7,24,28,15,17等数可组成一组直角三角形的三个边。
4、这也能让学生主动地参与到课堂中去,能起到激发学习兴趣的作用。 光有兴趣是不行的,还需要教师有好的教学方法。
我看勾股定律读后感200字
1、数学史读后感 篇1 从小到大,在学习数学的过程中,接触大量的数学题,对数学的历史很少提及。《数学史》,一本专门研究数学的历史,娓娓道来,满足了我的好奇,把数学的发展过程展示出来。 本书于1958年出版,作者J.F.斯科特。
2、《九章算术》读后感 篇1 《九章算术》在很多方面有突出的成就,反映了这一时期我国数学的发展水平。其成就最突出地表现在分数运算,比例问题和“盈不足”算法方面。
3、在周髀算经》和《九章算术》中都已明确给出了勾股定理的一般形式:勾+股=弦。
4、爱因斯坦读后感1 小时候,我曾问过爸爸:“世界上最聪明的人是谁?”爸爸说:“应该是爱因斯坦。”这不,现在我就借了《爱因斯坦》这本书。
5、我脑海中印象最深的就是那棵毕达哥拉斯树,它是由勾股定理不断的连接从而构成的一个树状的几何图形。两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。
数学史读后感
”在现代社会中,数学正在对科学和社会的发展提供着不可或缺的理论和技术支持。数学史不仅仅是单纯的数学成就的编年记录。
第三次数学危机,“罗素悖论”使数学的确定性第一次受到了挑战,彻底动摇了整个数学的基础,也给了数学更为广阔的发展空间。但歌德尔的不完全性定理却使希尔伯特雄心建立完善数学形式化体系、解决数学基础的工作完全破灭。
读了这本书,让我对数学学习有了 新的认识和感悟,也让我更深层次的了解到数学的魅力和伟大,以及 对前人的崇敬。数学源于人类的生活与发展。
到此,以上就是小编对于勾股定理感悟和收获的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

